Ook heb ik een poll laten rondgaan met terug enkele keuzes welk artikel er graag zou gelezen worden. Deze stond dan ook met kop en schouders boven de rest van de keuzes die later zullen aangevuld worden.
Analoog aan eerdere artikels zullen we een behoorlijke weg afleggen en spreken we terug over vorticiteit: een topic die in de meteorologie altijd en overal meespeelt en behandelen we de stretching & tilting die verantwoordelijk is om de horizontale vorticiteit afkomstig van de windschering te kantelen in de verticale zin en die door een updraft te stretchen.
De vorticiteits-aspecten "stretching" & "tilting" werden al uitvoerig behandeld in eerdere artikels, maar nu dienen we deze vanuit een ander perspectief te benaderen en de toepassing doelgericht te gebruiken om de origine van de supercel updraft rotatie te vinden. We zullen het daarom ook veel hebben over de wind in een "storm-relatief" framework en dus een passage invoeren over de notie van storm-relatieve wind en behandelen we het gevolg en de oorzaak van de afwijkende beweging die supercels hebben t.o.v. de normale buienbeweging.
Een hele waslijst dus. Vandaar dat dit artikel ietwat langer is dan eerdere blog-entries.
Zoals altijd betrek ik er graag wat wiskunde bij maar de formules zullen we vakkundig uit elkaar trekken om de aparte termen van elkaar te kunnen onderscheiden. Om dit artikel te begrijpen heb je dus géén wiskunde kennis nodig. Enkel (zoals altijd) een portie inbeeldingsvermogen die je zal helpen om de topics in dit artikel te visualiseren en als gevolg ook beter te begrijpen. Er zullen geen ingewikkelde berekeningen worden gemaakt, enkel gerefereerd naar een wiskundige notatie.
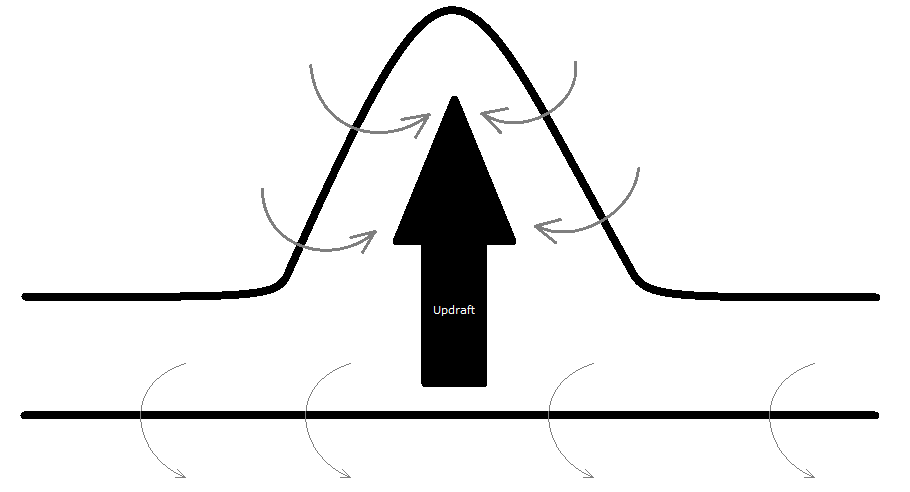
Nu... Om een roterende updraft te hebben dient onze updraft zich te bevinden in een gebied waar er verticale vorticiteit aanwezig is. Die vorticiteit wordt dan door een stijgstroom in de verticale zin uitgerokken die de vorticiteitskolom doet versmallen waardoor de rotatiesterkte wordt aangespannen. We hebben dit reeds behandeld in het artikel omtrent de tornadische supercel waar bovenstaande afbeelding vandaan komt.
In tegenstelling tot bovenstaande afbeelding waar de vorticiteit enkel in de onderste niveaus te zien is en zo door die "stretching" de non-supercel tornado zijn rotatie krijgt is de rotatie voor de supercel veel dieper en bevindt die zich vanaf de midlevels van 3 - 6km en afhankelijk van de buiendiepte zelfs veel hoger.
De ontwikkeling van supercels is dus van die verticale vorticiteit sterk afhankelijk. Heb je geen verticale vorticiteit of kan die niet gegenereerd worden, heb je ook onmogelijk een supercel, vandaar dat het belangrijk is om de "lokale verandering van verticale vorticiteit over tijd" te weten, wat ons brengt tot "de supercel-formule" (althans: ik noem die graag zo).
Wiskundig gezien is de "lokale verandering van de verticale vortictieit over tijd" de som van de vorticiteits-advectie van de aanwezige verticale vorticiteit (zeta) plus de stretching van de aanwezige verticale vorticiteit (zeta) plus de tilting (kanteling) van de aanwezige horizontale vorticiteit.
\[\frac{{\partial \zeta }}{{\partial t}} = - \vec V \cdot \nabla \zeta + \zeta \frac{{\partial w}}{{\partial z}} + {\vec \omega _H} \cdot {\nabla _H}w\]
Hieronder zie je dezelfde formule maar dan uit elkaar gehaald waarbij de verklaring in tekstvorm alles zal duidelijk maken, dus laat je vooral niet afschrikken door deze formule. Ze is best gemakkelijk te interpreteren.
Als we een stijgstroom hebben in een omgeving zonder verticale vorticiteit (verticale vorticiteit = zeta: de krul in de linker term) zien we een vermenigvuldiging met 0 in de eerste en tweede term na de "=". Logisch ook want als er geen verticale vorticiteit aanwezig is (zeta = 0) om mee te starten is er niets te stretchen en geen vorticiteit te advecteren. Vinden we wel vorticiteit aanwezig doorheen de atmosfeer wordt deze vorticiteit door de updraft gebruikt en wordt die vorticiteit dus gestretched in de verticale zin.
Hoe groter de aanwezige verticale vorticiteit des te groter ook de contributie van de verticale vortictieit aan de supercel-updraft rotatie... So far so good.
Hebben we echter géén of amper verticale vorticiteit aanwezig in de atmosfeer zijn de advectieterm & de stretching-term waardeloos en is de enige die de nodige verticale vorticiteit voor onze supercel updraft-rotatie kan opwekken de tilting-term in de vergelijking: vandaar ook het kadertje rond de laatste term. Merk trouwens op dat er zich de laatste term in de vergelijking geen "zeta" bevindt.
Dit is een héél belangrijk punt. De stretching- en de advectieterm zijn positief en hebben betekenis als er verticale vorticiteit aanwezig is en het ènige proces dat verticale vorticiteit kan genereren is het tilting-proces van de horizontale vorticiteit in de verticale zin.
We weten ondertussen al dat de horizontale vorticiteit wordt opgewekt door de windschering.
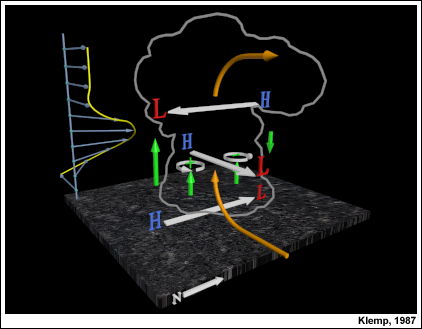
We zien in bovenstaande afbeelding een windscheringsprofiel waarbij de west-oost wind met hoogte in snelheid toeneemt en noemen dit westerlijke schering. Omwille van die snelheidstoename vinden we dus niet verwonderlijk ook horizontale vorticiteit. We zien een snelheidstoename van de west-oost wind (U-component van de wind = du/dz) met hoogte. Wanneer we hoger gaan in hoogte (z) gaat "u" ook omhoog dus...
\[\frac{{\partial \vec u}}{{\partial z}} = positief\]
Als er een stijgstroom is, er ontwikkelt er zich ene in dit horizontaal vorticiteitsveld of dit horizontaal vorticiteitsveld trekt over de plaats van een bestaande onweersbui (m.a.w. de windschering spant aan over een bestaande convectieve gebeurtenis) buigt de stijgstroom deze horizontale vorticiteit om in een verticale zin en wordt die dus gekanteld. Dit is het "tiltingsproces".
De volgende afbeelding toont dit treffend waarbij we starten met de horizontale vorticiteit afkomstig van de windschering en de updraft die de vortexlijn in de verticale zin kantelt.
Een vortexlijn moet je zien als een lijn die niet kan gebroken worden. Het is een onbreekbare lijn in een vloeistof dus als die updraft die vortexlijn kantelt blijft die intact en krijg je aan de linkerzijde en rechterzijde van de stijgstroom verticale vorticiteit waarbij je aan de linkerzijde van de updraft cyclonale vorticiteit ziet en aan de rechterzijde anticyclonale.
Bekijken we ditzelfde concept maar dan vanuit het bovenaanzicht zien we diezelfde 2 vortices met de updraft in het midden. We zullen deze updraft de thermodynamische updraft noemen. De reden dat we dit onderscheid maken wordt later duidelijk, maar het sleutelpunt tot hier toe is dat de thermodynamische stijgstroom verantwoordelijk is voor de tilting van de horizontale vortexlijn in de verticale zin, wat ons brengt tot onderstaand bovenaanzicht van hetzelfde gegeven.
Onthoud dat dit mechanisme spreekt over de generatie van de verticale vorticiteit in de midlevels en dus de mid-level mesocycloon. Ontwikkeling van verticale vorticiteit in de low levels die bevorderlijk is voor de low-level mesocycloon is een ander mechanisme maar dit hebben we reeds besproken in het artikel over de tornadische supercel.
Bekijken we dit vorticiteits-paar in de context van een echte onweersbui komen we tot de volgende stap en zullen we de tilting & stretching toepassen op een echte bui en bespreken we de implicaties van de thermodynamische updraft-interactie met de oorspronkelijke horizontale vorticiteit.
We zien links het storm-relatief windprofiel dus hebben we westerlijke storm-relatieve windschering met een toename in de windsnelheid richting het oosten hoe hoger in de atmosfeer. Mochten we grond-relatieve wind willen illustreren zou de lijn aan de tip van de windvectoren beginnen aan de oorsprong onderaan en in de richting van de windschering (oostelijk) doorbuigen tot bovenaan de atmosfeer.
De bui beweegt richting het oosten, uit het scherm. Wanneer de bui dus richting het oosten beweegt ondervindt die ook inflow vanuit het oosten, wat duidelijk te zien is aan het storm-relatief windprofiel linksboven.
Plaatsen we zoals vermeld een tube in dit scheringsprofiel zien we dat deze zal roteren in de richting die aangeduid is door de groene rotatiepijlen rond de vortexlijnen die werden aangeduid door de annotatie. Wanneer we om welke reden dan ook een updraft triggeren in dit shearprofiel zien we dat de vortexlijn wordt getilt in de verticale zin met ten zuiden van het udpraft maximum de cyclonale vorticiteit en ten noorden van onze stijgstroom de anticyclonale rotatie.
De vraag wordt dus hoe we hieruit een cyclonaal roterende supercel krijgen. Op dit ogenblik kunnen we nìet spreken van een supercel want de netto rotatie is 0 aangezien we evenveel cyclonale als anticyclonale vorticiteit hebben aan de flank van de thermodynamische updraft.
Links vinden we de een cirkel met een "+" en rechts een cirkel met een "-". Cyclonale vorticiteit vinden we dus links en de anticyclonale zin rechts met in het midden de thermodynamische updraft. Het punt is dat er evenveel positieve als negatieve rotatie in de updraft zit met als resultaat dat als we de gehele vorticiteit integreren over de volledige diepte en gebied van de updraft er geen netto rotatie te vinden is.
Met de thermodynamische updraft symmetrisch in het midden en een nulwaarde aan netto-rotatie kunnen we dus niet spreken over een supercel. We hebben géén mesocycloon. We moeten dus iets doen aan onze bui om de bui tot supercel te doen evolueren...
Je vraagt je misschien af waarom in het model de 2 gestippelde gele pijlen zijn getekend die richting het centrum van die vortices wijzen.
De reden waarom is dat het drukveld in die vorticiteit in principe een "cyclostrofisch gebalanceerde vortex" is. Dat betekent dat ongeacht zijn rotatie-richting de druk wordt verlaagd. Je zou daar eigenlijk een "L" als label kunnen plaatsen omwille van die drukverlaging. We noemen deze lagedrukveldjes LPG's of "Lifting Pressure Gradiënts" vanwege de "Lifting Pressure Gradient Force".
Het resultaat is dat je 2 soorten updrafts hebt in deze onweerswolk. We hebben zoals gezegd de thermodynamische updraft - thermodynamisch omdat die gedreven wordt door de latent-heat release van de condensatie - en omwille van die LPG's ook een dynamische updraft, waarbij de term "dynamisch" wijst op het dynamische systeem waardoor de 2 lagedrukvelden worden gecreëerd. Die kernen van lage druk komen er door beweging, meerbepaald rotatiebeweging: niet door de vrijlating van latente warmte.
Hierdoor hebben we ook bewezen dat de "supercel-split" eigenlijk een illusie is, aangezien de thermodynamische updraft 2 dynamische updrafts ontwikkelt. We krijgen dus op een gegeven moment 3 buienkernen voor de prijs van 1.
Een goede vraag zou zijn waarom die gele pijlen naar omhoog worden getekend. Kan het niet zijn dat die pijlen horizontaal van buiten naar binnen of zelfs van boven naar beneden moeten getekend worden? In principe is dat inderdaad zo dat dit laag wordt "opgevuld" langs alle kanten, maar omwille van de warme omgeving en de hoge vochtigheid onderaan waaruit de thermodynamische updraft gebeurt en het feit dat we reeds verticale beweging hebben (thermodynamische updraft) geeft ons een netto-aanvoer van onder naar boven richting het centrum van die LPG's.
Nogmaals: in dit voorbeeld is er omwille van dit vortex-paar géén netto rotatie. In de noordelijke hemisfeer is de updraft van een supercel dominant cyclonaal. Waarom? Het antwoord vinden we in het concept "storm-relatieve wind". We zullen zien dat het ènige, maar dan ook het ènige dat telt op vlak van supercel updraft dynamics de storm-relatieve wind is.
We moeten om de storm-relatieve wind te begrijpen terug gaan naar de basisfysica. Als iemand een bal gooit en die staat op een kar die vooruit rolt gaat de absolute snelheid van de bal gelijk zijn aan de snelheid waaraan de bal wordt gegooid + de snelheid van de kar waarop de persoon staat die de bal gooit.
Passen we dit concept toe op de atmosfeer zien we net hetzelfde. Denk aan jezelf op de fiets. Als jij met de fiets aan 20km/u vooruit rijdt en je hebt de wind in de rug aan 30km/u ondervind je een meewind aan 10km/u. Fiets je daarentegen aan een 20km/u en je hebt de wind in uw rug aan 20km/u zal je vanuit uw perspectief (fiets-relatief als het ware) de atmosfeer als kalm aanvoelen en zal het "windstil" zijn.
Fiets je aan 20km/u en je ondervindt de wind ditmaal van voor aan een 50km/u, vind je het steevast moeilijker om vooruit te geraken en ondervind jij een wind van 70km/u. Dit is namelijk de meest ideale configuratie voor de bui, waarbij de bui zelf een tegenwind ondervindt. De reden hiertoe wordt direct duidelijk, maar hieronder ziet u alvast enkele voorbeelden zoals hier met de fiets aangehaald in de context van een bui.
Net zoals het voorbeeld op de fiets vinden we hierboven hetzelfde concept maar dan in de context van een bui. Net zoals de fiets is de bui nu het coördinatensysteem. De verdere bespreking in dit artikel dient altijd meegaand met de bui benaderd te worden. Beeld je als het ware in dat je jezelf in de storm bevindt of dat jij zelf de bui bent.
In het eerste voorbeeld zien we dat de bui van links naar rechts aan een 40kts vooruit beweegt terwijl de wind in de omgeving ook van links naar rechts beweegt aan 20 kts. Storm-relatief ondervindt de bui dus een tegenwind aan 20 kts (denk aan het fiets-voorbeeld). In het tweede voorbeeld zien we de case waarbij de bui geen wind voelt aangezien de bui aan dezelfde snelheid & richting voortbeweegt als de wind van de omgeving.
Het laatste voorbeeld is daarentegen de optimale situatie waar de bui van links naar rechts beweegt en de wind in tegengestelde richting raast. Hierdoor ondervindt de bui een sterke storm-relatieve wind.
En hier komt het allerbelangrijkste punt van dit artikel: Een sleutelpunt voor supercel-onweersbuien is sterke low-level storm-relatieve wind. Wat een profiler of sounding benadert is de grond-relatieve wind. Nogmaals: Deze zijn volstrekt onbelangrijk. Het ènige dat telt op vlak van supercel-updraft dynamica is de storm-relatieve wind... Je hebt natuurlijk grond-relatieve windobservaties nodig om de storm-relatieve wind te kunnen weten, maar op vlak van supercel-updraft dynamics zijn die onbelangrijk.
Het is wat de bui zèlf ondervindt dat belangrijk is om de generatie van een supercel-updraft mogelijk te maken! Niet de grond-relatieve wind van de omgeving!
Wanneer we terug gaan naar onze 2 cyclostrofisch gebalanceerde vortices onthouden we dat we ten tijde van dit beeld nog geen supercel hebben omwille van de afwezigheid van een netto rotatie. Er is evenveel LPGF (Lifting Pressure Gradiënt Force) in de linker als de rechter vortex.
We weten uit observatie dat in de noordelijke hemisfeer de meeste supercels cyclonaal zijn, vandaar ook de naam "mesocycloon". De vraag hoe we uit deze situatie nu een supercel krijgen (lees: een mesocycloon) blijft tot nu toe nog steeds onbeantwoord. Het is hier dat de storm-relatieve wind om de hoek komt kijken.
De notie is dat als de bui richting het oosten beweegt dat de bui ook een storm-relatieve inflow vanuit het oosten ondervindt. Als we een mesocycloon willen genereren moeten we dus een netto-rotatie ontwikkelen. Wat we dus moeten doen is de linkervortex (zuidelijke) sterker laten spinnen dan de rechtervortex (noordelijke).
De meest efficiënte manier om dit te doen is wat? Stretching, niet?
Met andere woorden dienen we dus een stretching te genereren in de zuidelijke vortex om diens rotatie sterker te laten aanspannen dan de noordelijke. Wat is stretching? Die vortex dient uitgerokken te worden wat we kunnen bekomen door de updraft van de bui te verplaatsen naar de plaats waar de cyclonale LPG zich bevindt.
Nu... Je kan moeilijk de bui vastnemen en die gewoon enkele kilometer verplaatsen maar wat we daarentegen wel kunnen doen is het volgende.
Eerder bewoog de bui dus uit het scherm richting het oosten en ondervond de bui dus die oostelijke storm-relatieve inflow met als resultaat géén netto-rotatie. Laten we de bui daarentegen in een zuidelijke richting trekken, verschuift de storm-relatieve wind (inflow) ook richting het zuiden.
En dit is precies wat we willen! Hierdoor wordt de zuidelijke vortex sterker gestretched dan de noordelijke. Nu dat de storm-relatieve inflow uit het zuiden komt of een zuidelijk component heeft door het zuidelijk component van de trekrichting gebeuren er eigenlijk 2 dingen. We hebben de tilting van de horizontale vorticiteit in de verticale zin en tegelijkertijd stretchen we de cyclonale vortex...
Wat ons brengt tot een ander sleutelpunt in het supercel-verhaal: stroomsgewijze vorticiteit.
Merk op dat de nu zuidelijke storm-relatieve inflow parallel is met de vortexlijnen! Dit is de meest optimale situatie dat je kunt verkrijgen. Wanneer de storm-relatieve inflow parallel loopt met de vortexlijnen noemen we dit optimale stroomsgewijze vorticiteit die in de cyclonale LPG wordt gepompt.
Met andere woorden: de zuidelijke storm-relatieve inflow en stroomsgewijze vorticiteit zijn sterk gecorreleerd en daardoor krijgen we onze netto-rotatie door op een efficiënte manier de spin van de cyclonale LPG aan te sterken door middel van "selectieve stretching".
Hoe meer dat de storm-relatieve inflow parallel loopt met de low-level vortexlijnen hoe sterker de stroomsgewijze vorticiteit (stroomsgewijs wijst op hoe parallel de inflow & vortexlijnen zijn) en hoe efficiënter de simultane tilting & stretching van de cyclonale vortex is, wat op zijn beurt dan ook resulteert in een sterkere en vluggere switch van onweersbui naar supercel. De sterkte van de storm-relatieve inflow heeft dus sterke invloed op de sterkte en levensduur van een supercel met dezelfde eigenschap: hoe sterker die inflow, hoe heviger de supercel zal zijn.
In het verhaal van de supercel kan je dus onmogelijk rond die storm-relatieve wind heen!
Terwijl de zuidelijke LPG wordt gestretched gebeurt met de noordelijke LPG net het tegenovergestelde. Aangezien de storm-relatieve inflow langs de vortexlijn gaat werkt deze de noordelijke opwaartse LPGF tegen en begint de noordelijke vortex samengedrukt te worden. Het resultaat is natuurlijk dat die noordelijke vortex afzwakt wat ook de reden is dat de leftmover zwakker wordt terwijl de rightmover intenser wordt.
Belangrijk te onthouden is dat de stroomsgewijze vorticiteit op die manier optimaal is omdat het leidt tot de onmiddellijke selectieve stretching van één bepaalde vortex t.o.v. de andere.
We hebben het nog niet gehad over hoe de storm-relatieve wind ineens vanuit het zuiden zou kunnen komen of waarom plots de bui in een andere richting zou bewegen. We weten dat een supercel-initiatie wordt voorafgegaan door een split en dat de right of leftmover veelal overblijft.
Wanneer een bui begint te "rightmoven" vinden we hierbij dus de reden (let op: de reden! niet de oorzaak maar de reden) waarom supercels ineens zo intens worden wanneer zij naar rechts beginnen afwijken. Hierdoor verschuift de storm-relatieve inflow in de richting waar ze naartoe beweegt en voedt die rechtstreeks de cyclonale LPG waardoor we ineens van een krachtige bui naar een monsterlijke mesocycloon en/of een tornadische onweersbui overgaan.
Waarom begint nu plotseling een bui af te buigen en verschuift die low-level storm-relative inflow ineens naar een betere positie?
Bovenstaande afbeelding is een afbeelding van een hypothese van Newton & Frankhauser (1964). Dit concept is een theorie die later werd ontkracht en is een analogie aan de flow rond een obstakel.
De zuidelijke vectoren onderaan stellen een zuidelijke wind voor en de vectoren links die naar rechts wijzen stellen de wind voor in de upper levels (vandaar Vl & Vu). Dus we zien hier daadwerkelijk een windprofiel waarbij de wind in hoogte draait en eventueel aansterkt: veering dus.
De storm-motion zijn de vectoren in stippellijn. De relatieve inflow is de dubbele pijl die je rechts onder ziet. de hyopthese was dat je sterke convergentie hebt in de plaats van de toren (rechts) en dat het door discrete propagatie aangroeit aan de rechterkant. Dus in plaats van naar rechts af te buigen groeide de bui gewoon aan langs de rechterkant, maar deze theorie werd ontkracht.
Een andere hypothese die naar voor werd gebracht was deze van het Magnus effect.
Het idee hierachter is dat wanneer je een roterend object hebt in een flow van links naar rechts er een lagere druk gecreëerd wordt op de locatie waar de flow in de zelfde richting vloeit als de rotatie door de accumulatie van beide snelheden en een hogere druk in de locatie waar de rotatierichting van het object in de tegengestelde richting is van de flow.
Hierdoor wordt via het Bernoulli effect een PGF (Pressure Gradient Force) opgesteld van hoge naar lage druk met als resultaat de afwijkende beweging van de bui richting de lagere druk.
Ook deze theorie werd ontkracht. Nochthans werkt deze theorie in het concept van een voetbal die je een curvend traject kan geven, maar we weten dat een bui geen vast object is. Vandaar dat ook deze theorie niet staande bleef.
Tot slot kwam er een hypothese van Rotunno & Klemp in 1982, namelijk de lineaire theory van een geïsoleerde updraft.
Deze theorie is diegene die tot op de dag van vandaag nog steeds staande blijft en het idee erachter is dat er door een veeringsprofiel (wind die wijzers-in draait met hoogte) een variabele drukverdeling wordt opgewekt.
Die verdeling is zo dat we aan de linkerkant (zuidelijk in het schema) in de lage niveaus een hoge druk hebben en een lage druk bovenaan, terwijl dat aan de noordelijke kant net het tegenovergestelde is. Hierdoor vinden we aan de zuidkant een verticaal PGF waardoor we langs de zuidkant een verticale aangroei vinden van nieuwe updraft impulsen terwijl we in de hogere niveaus een PGF vinden van noord naar zuid.
Deze 2 zijn volgens Rotunno & Klemp de 2 drijvende factoren achter de afwijkende beweging richting het Z of toch tenminste propagatie met een zuidelijk component. Belangrijk om weten is dat deze theorie nog altijd niet bewezen of ontkracht is, maar dat deze (tot vandaag de dag) de meest plausibele is en diegene is die als "waar" aanzien wordt.















Geen opmerkingen:
Een reactie posten